Équation de la consolidation
en une dimension selon Terzaghi (1923)
Table des matières
- Hypothèses
- Relation constitutive
- Contrainte effective
- Variation de volume
- Loi de Darcy (1856)
- Références
- Notations
Le comportement du sol lors de la consolidation est régi dans le plus simple des cas par l'équation différentielle de consolidation unidimensionnelle, développée par Terzaghi (1923). Dans cette sous-section, nous allons démontrer cette équation, en commençant par énoncer ses hypothèses.
Hypothèses
Les neuf hypothèses de la théorie hydrodynamique de Terzaghi sont les suivantes (Taylor, 1948) :
- Le sol est homogène ;
- Le sol est saturé – il n'y a que deux phases: l'eau et le squelette solide ;
- Les phases liquides et solides sont incompressibles – la déformation du sol se produit de par l'expulsion ou l'apport d'eau qui est contrebalancée par un réarrangement du squelette solide ;
- Les déformations sont infinitésimales mais représentatives d'un élément de sol de dimension finie ;
- Le débit d'eau se produit selon une direction – la direction $z$ sans perte de généralité ;
- Les déformations du squelette se produisent selon la direction $z$ uniquement – nous sommes donc en conditions œdométriques ;
- L'eau s'écoule au travers du squelette du sol selon la loi de Darcy (1856) : \begin{equation} v_a = ki\label{eq:def-loi-darcy-chap-comp} \end{equation} avec: \begin{equation} i = \frac{-\udelta h}{\udelta l} \end{equation} où $k$ est la perméabilité du sol et $i$ le gradient hydraulique du sol qui représente la perte de charge $\udelta h$ sur le chemin parcouru $\udelta l$ ;
- Le sol est élastique; le rapport entre la déformation verticale et la contrainte effective verticale est constant et est exprimé par le coefficient de changement de volume : \begin{equation} m_v' = \frac{\udelta\varepsilon_z}{\udelta\sigma_z'}\label{eq:def-mv-chap-comp} \end{equation}
- En plus d'être constantes dans l'espace, la perméabilité ($k$), le coefficient de changement de volume ($m_v'$) et le poids volumique de l'eau ($\gamma_w$) sont considérés constants en fonction de la contrainte effective ou du temps.
Les trois premières hypothèses sont classiques et sont assez fidèles de la réalité. La quatrième hypothèse est académique; d'une part, les déformations infinitésimales sont acceptables pour les niveaux de tassement généralement observés et d'autre part, le sol étant bi-phasique, une action qui se produirait sur un distance infinitésimale ne serait pas représentative d'un plus grand volume, contenant solide et eau. La cinquième et sixième hypothèse sont valides en laboratoire; sur site néanmoins, leur degré de validité doit être évalué. La septième hypothèse peut être acceptée sans grande remise en cause. La huitième hypothèse par contre est la plus pénalisante, c'est elle qui engendre la limitation de validité de cette théorie (Taylor, 1948) ; une discussion de cette hypothèse est faite ici (lien manquant). Finalement, la neuvième hypothèse est source de divergence mais le plus souvent mineure.
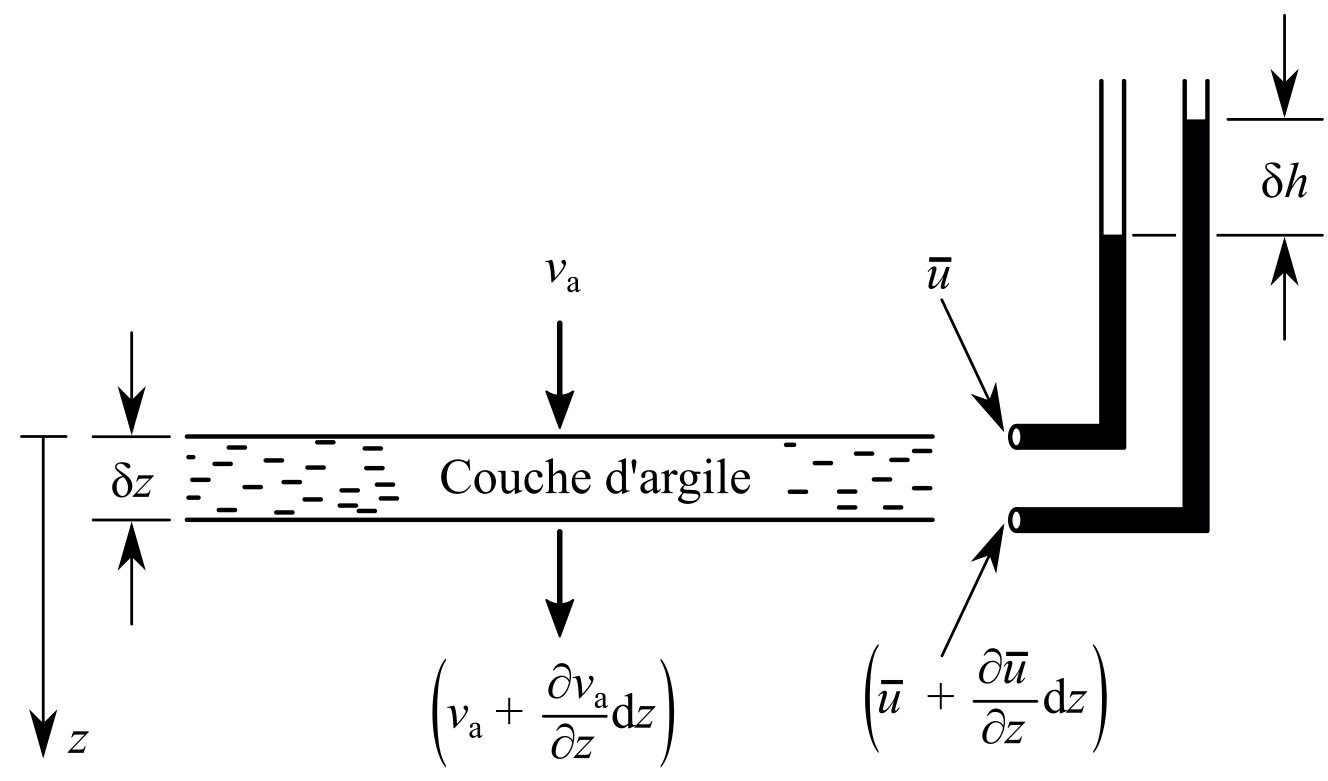
Nous considérons un horizon de sol saturé en conditions œdométriques illustré à la figure 1. Cet horizon a les conditions initiales suivantes: une contrainte verticale totale $\sigma_{z0}$, une pression interstitielle $u_0$ et donc une contrainte verticale effective $\sigma_{z0}' = \sigma_{z0} - u_0$. L'épaisseur de cette couche est $\udelta z$ et l'aire de sa section transversale est $A$.
Au temps $t=0$, on soumet l'horizon à un incrément de contrainte totale ($\udelta \sigma_z$) maintenu constant. À partir de ce temps, la contrainte totale de l'horizon est constante, $\sigma_z = \sigma_{z0} + \udelta \sigma_z$, et ce sont la contrainte effective ($\sigma_z' = \sigma_{z0}' + \udelta \sigma_z'$) et la pression interstitielle ($u = u_0 + \excess{u}$) qui vont varier.
Dû à la variation de pression interstitielle et de contrainte effective, l'horizon va subir un tassement $\udelta s_c$, c'est-à-dire une variation de son épaisseur (qui sera négative), pendant l'intervalle de temps $\udelta t$. D'après les hypothèses reprises ci-dessus, ce tassement est uniquement dû à l'expulsion d'eau.
La démonstration de l'équation de consolidation selon Terzaghi (1923) se réalise en quatre étapes qui sont détaillées ci-dessous.
Relation constitutive
L'incrément de déformation volumique ($\udelta \varepsilon_v$) peut être exprimé par :
\begin{equation} \udelta \varepsilon_v = \frac{-\udelta V}{V} \label{eq:cons-terz-demo-depsv} \end{equation}où $\udelta V$ est la variation de volume de l'horizon et $V = A\udelta z$ son volume.
Vu que nous sommes en conditions œdométriques, la seule déformation est la déformation verticale, ce qui nous permet d'écrire que : \begin{equation} \udelta \varepsilon_v = \udelta \varepsilon_z \label{eq:cons-terz-demo-depsv-depsz} \end{equation}
En utilisant la relation constitutive définie à l'équation \eqref{eq:def-mv-chap-comp}, les équations \eqref{eq:cons-terz-demo-depsv} et \eqref{eq:cons-terz-demo-depsv-depsz} se transforment en :
\begin{equation} \udelta V = - m_v V \udelta \sigma'_z \end{equation}ce qui donne, pour un incrément infinitésimal de temps, la variation suivante :
\begin{equation} \frac{\partial V}{\partial t} = - m_v V \frac{\partial \sigma'_z}{\partial t} \label{eq:cons-terz-demo-part1} \end{equation}Contrainte effective
L'incrément de contrainte totale ($\udelta \sigma_z$) est maintenu constant, de telle sorte que l'on puisse écrire :
\begin{equation} \udelta \sigma_z = \udelta \sigma_z' + \excess{u} = \text{constante} \label{eq:cons-terz-demo-deltasigmazeff-deltau} \end{equation}Dès lors, en prenant la dérivée par rapport au temps, on peut écrire:
\begin{equation} \frac{\partial \left(\udelta\sigma_z'\right)}{\partial t} + \frac{\partial \excess{u}}{\partial t} = 0 \end{equation}ou, en prenant en compte le fait que $\sigma_z' = \sigma_{z0}' + \udelta\sigma_z'$ où $\sigma_{z0}'$ est constant :
\begin{equation} \frac{\partial \sigma_z'}{\partial t} = - \frac{\partial \excess{u}}{\partial t} \label{eq:cons-terz-demo-part2} \end{equation}Variation de volume
La variation de volume de cet horizon est égal à la différence entre la quantité d'eau entrante et sortante (Taylor, 1948) :
\begin{equation} A v_a - A \left( v_a + \frac{\partial v_a}{\partial z} \udelta z \right) = \frac{\udelta V}{\udelta t} \label{eq:cons-terz-demo-deltaVdeltat} \end{equation}En se souvenant que $V=A\udelta z$, l'équation \eqref{eq:cons-terz-demo-deltaVdeltat} se devient, pour un incrément de temps infinitésimal :
\begin{equation} - V \frac{\partial v_a}{\partial z} = \frac{\partial V}{\partial t} \label{eq:cons-terz-demo-part3} \end{equation}Loi de Darcy (1856)
A la limite, l'équation \eqref{eq:def-loi-darcy-chap-comp} devient :
\begin{equation} v_a = ki = -k \frac{\partial h}{\partial z} = \frac{-k}{\gamma_w} \frac{\partial \excess{u}}{\partial z} \label{eq:cons-terz-demo-part4} \end{equation}Nous pouvons maintenant conclure la démonstration, en regroupant les équations \eqref{eq:cons-terz-demo-part1} et \eqref{eq:cons-terz-demo-part2} :
\begin{equation} \frac{\partial V}{\partial t} = m_v V \frac{\partial \excess{u}}{\partial t} \label{eq:cons-terz-demo-end-1} \end{equation}et d'autre part les équations \eqref{eq:cons-terz-demo-part3} et \eqref{eq:cons-terz-demo-part4} :
\begin{equation} \frac{\partial V}{\partial t} = V \frac{k}{\gamma_w} \frac{\partial^2 \excess{u}}{\partial z^2} \label{eq:cons-terz-demo-end-2} \end{equation}En regroupant les équations \eqref{eq:cons-terz-demo-end-1} et \eqref{eq:cons-terz-demo-end-2}, on obtient l'équation de consolidation unidimensionnelle selon la théorie de Terzaghi (1923) :
\begin{equation} \frac{\partial \excess{u}}{\partial t} = c_v \frac{\partial^2 \excess{u}}{\partial z^2} \label{eq:consolidation-1d-terzaghi} \end{equation}où $c_v$ est le coefficient de consolidation (coefficient of consolidation), qui a les unités m²/s et vaut :
\begin{equation} c_v = \frac{k}{m_v' \gamma_w} \label{eq:coefficient-de-consolidation} \end{equation}et où $k$ est la perméabilité dans la direction $z$, $m_v'$ le coefficient de changement de volume défini à l'équation \eqref{eq:def-mv-chap-comp} et $\gamma_w$ le poids volumique de l'eau.
L'équation \eqref{eq:consolidation-1d-terzaghi}, qui est une équation de la chaleur, est très utilisée pour résoudre rapidement des problèmes de consolidation.
Références
- Henry DARCY : Les fontaines publiques de la ville de Dijon. Victor Dalmont, Paris, France, 1856.
- Andrew N. SCHOFIELD et C. Peter WROTH : Critical State Soil Mechanics. McGraw- Hill, Maidenhead, Royaume-Uni, 1968.
- Donald W. TAYLOR : Fundamentals of Soil Mechanics. John Wiley & Sons, Inc., Londres, Royaume-Uni, 1948.
- Karl TERZAGHI : Die berechnung der durchlässigkeitsziffer des tones aus dem verlauf der hydrodynamischen spannungserscheinungen. Akademie der Wissenschaften in Wien, Mathematish-Naturwissen-Schaftiliche Klasse, 132:125–138, 1923. (reproduit dans ‘From Theory to Practice in Soil Mechanics’ de Bjerrum et al., eds., pp. 133–146, 1960).
Notations
L'indice $0$ est utilisé pour dénoter les conditions intiales et l'exposant $'$ se rapporte à une quantité en rapport avec les contraintes effectives (et non totales).
Un petit incrément est précédé par le symbole $\udelta$. La dérivée totale est indiquée par le symbole $\ud$ et la dérivée partielle par le symbole $\partial$.
| Symbole | Unité | Description |
|---|---|---|
| $A$ | m² | Aire de la section |
| $c_v$ | m²/s | Coefficient de consolidation |
| $h$ | m | Hauteur de charge |
| $i$ | – | Gradient hydraulique |
| $k$ | m/s | Coefficient de perméabilité |
| $m_v'$ | m²/kN | Coefficient de changement de volume |
| $s_c$ | m | Tassement dû à la consolidation |
| $t$ | s | Temps |
| $u$ | kPa | Pression interstitielle |
| $\excess{u}$ | kPa | Excédent de pression interstitielle |
| $v_a$ | m/s | Vitesse apparente de Darcy |
| $V$ | m³ | Volume |
| $z$ | m | Position verticale |
| $\udelta$ | Petit incrément | |
| $\varepsilon_v$ | – | Déformation volumique |
| $\varepsilon_z$ | – | Déformation verticale |
| $\gamma_w$ | kN/m³ | Poids volumique de l'eau |
| $\sigma_z'$ | kPa | Contrainte verticale effective |
| $\sigma_z$ | kPa | Contrainte verticale totale |
| $~$ |